Number Of Distinct Poker Hands
Understanding Probability In Texas Holdem Is An Essential Aspect Of Profitable Play
– Pre-Flop Probability Guide
Number Of Distinct Poker Hands Signals
An Introduction to Thermal Physics Daniel V. Schroeder Problem 2-4 Calculate the number of different 5-card poker hands selected from a standard deck of 52 c. In poker, players form sets of five playing cards, called hands, according to the rules of the game. Each hand has a rank, which is compared against the ranks of other hands participating in the showdown to decide who wins the pot. In high games, like Texas hold 'em and seven-card stud, the highest-ranking hands win. The number of distinct 5-card poker hands that are possible from 7 cards is 4,824. Does anyone have the break down of the 4,824? A list of the 4824? Better yet a program to generate the 4824? You don't subtact this from the total number of permutations, you divide it, because each possible combination of hands has these possible 'duplicate' hands that we want to weed out from the total. So you have: 52 x 51 x 50 x 49 x 48-5 x 4 x 3 x 2 x 1. It has the same amount of numbers on the top as the bottom - the number of cards you drew. A good compromise would simply be to count the number of distinct values in the set of five 3, 14. Namely, corresponding to the classical Poker test that uses hands of five numbers we get five categories, 1different, 2different, 3 different, 4 different and 5 different. Thus, a finite time.

Ever wondered how often you will be dealt Aces? Or what the chances of facing an over-pair are when you hold Jack-Jack? This section of the site will give you the probability of certain hands before the flop (this page) and in later pages the chances of certain flops (for example one suit flop probability) and the chances of dominating hands being out there to your ace-x hand (where x is one of several small to medium cards).
We start by looking at how the cards in the deck can be dealt based on a random distribution of the 1326 ways of 2 cards falling and how often you’ll expect to be dealt certain hands. Then we take suitedness into account – since there are less ways of being dealt 2 suited cards. Later articles in this series will continue with the essential poker probability and card distribution stats you need.
Poker Calculator Pro: Did you know there is a software tool, approved by all the major rooms which will do all the odds, outs and equity math for you in real time? Poker Calculator Pro is the flagship tool of the cutting edge Pro Poker Labs. Check out Poker Calculator Pro for yourself now!
Firstly, where did the number 1326 come from? Well with 52 cards in the deck your first card is 1/52 this is then multiplied by 1/51 and the total divided by 2 (since it does not matter what order your cards are dealt in) giving 1326 combinations of all cards in any suit.
Of course suitedness is not often important, especially for low cards. The next question is then – what is the number of unique starting hands in Texas Holdem, not counting suits? The answer here is 169 unique hands.
Pre-Flop Poker Probability - 169 Distinct Starting Hands
Now we are getting somewhere. Next we can use the numbers above to work out what the probability of being dealt AA, KK (or in fact any pair) is. This is a case of taking the total number of possible hands and then seeing how many of these are your pair. We will take a pair of Kings as an example. Of the 1326 possible combinations there are 6 ways of being dealt this hand pre-flop. The 6 combinations possible are Kh-Kd, Kh-Kc, Kh-Ks, Kd-Kc, Kd-Ks and Kc-Ks.
6 / 1326 = 0.00435 or 221-to-1
So the chances of being dealt any specific pair are 221:1 against, in fact with 13 possible pairs the chances of being dealt any pair go up to 16-to-1 (there are 78 pair combinations from 1326 total).
Next we can look at unpaired hands, a specific example is the number of ways of being dealt Ace-king pre-flop. Here we have more possible combinations, since there are 8 cards that can be dealt first and then 3 remaining cards to make this hand (we will ignore suitedness for the moment). This gives 16 ways in which A-K can be dealt out of the 1326 combinations – a probability of 0.0121% or approximately 82-to-1. In fact this is the same for any unpaired hand when you ignore the suits.
Pre-Flop Poker Probability - Probability Of Hands Pre-Flop Chart
The reference table below gives probabilities of being dealt specific hands pre-flop: The next article in this series will look at the chances of being dealt hands at the same time as one or more opponent is dealt a higher hand – for example AA vs KK and AK vs QQ.
Pre-flop Hand | Odds | |
AA | 0.045 | Same for any pocket pair |
AK (any suits) | 0.012 | Any 2 cards not inc. suits |
AK (suited) | 0.003 | |
Pair 10-10 or better | 0.023 | 10-10, JJ, QQ, KK or AA |
AK, AQ or AJ | 0.036 | Suits not considered |
2 Suited Cards 10+ | 0.03 | |
Any Suited Connector | 0.039 | 23 suited or better |
2 Cards Jack + | 0.09 | Suits not considered |
Finally we can look at how combinations of pre-flop hands work, asking the question what is the probability of being dealt a playable hand for each position. We will use arbitary early, middle and late position combinations here to demonstrate – the actually hands you play is up to your personal style!
Position | Combinations | ||
Early Position | AA to JJ, AKo, AQs | 46 | 29:1 |
Early Mid Position | AA to 99, AQo+, AJs | 18:1 | |
Mid Position | 77+, A10o+ A8s+ KQ+ | 140 | 9,5:1 |
Late Position | 55+, A7+, QJo+, 78s+ | 5,5:1 |
Mark's Rec: Did you know that poker software tools are available which automatically calculate the math, leaving you to outplay your opponents? Poker Calculator Pro from the awesome Pro Poker Labs is the world's best poker calculator- and is approved by all the major poker sites – it can literally transform your profits overnight! Read our Poker Calculator Pro Review now to find out how…
Related Articles
Brian Alspach
13 January 2000
Abstract:
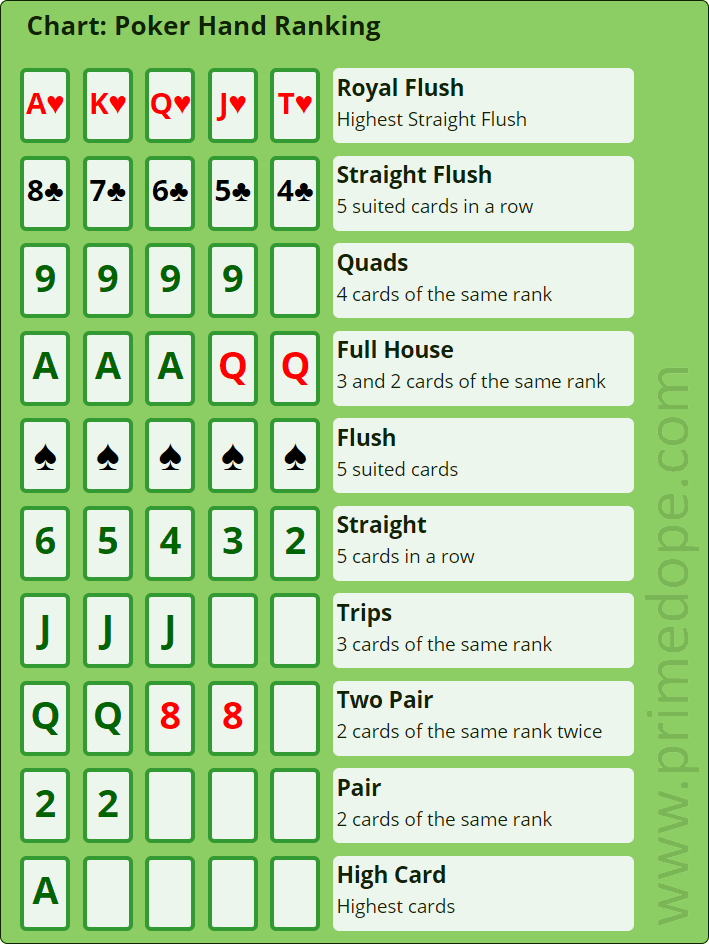
The types of 5-card poker hands are
- straight flush
- 4-of-a-kind
- full house
- flush
- straight
- 3-of-a-kind
- two pairs
- a pair
- high card
Most poker games are based on 5-card poker hands so the ranking ofthese hands is crucial. There can be some interesting situationsarising when the game involves choosing 5 cards from 6 or more cards,but in this case we are counting 5-card hands based on holding only5 cards. The total number of 5-card poker hands is.
A straight flush is completely determined once the smallest card in thestraight flush is known. There are 40 cards eligible to be the smallestcard in a straight flush. Hence, there are 40 straight flushes.
In forming a 4-of-a-kind hand, there are 13 choices for the rank ofthe quads, 1 choice for the 4 cards of the given rank, and 48 choicesfor the remaining card. This implies there are 4-of-a-kind hands.
There are 13 choices for the rank of the triple and 12 choices for therank of the pair in a full house. There are 4 ways of choosing thetriple of a given rank and 6 ways to choose the pair of the other rank.This produces full houses.
To count the number of flushes, we obtain choicesfor 5 cards in the same suit. Of these, 10 are straight flushes whoseremoval leaves 1,277 flushes of a given suit. Multiplying by 4 produces5,108 flushes.
The ranks of the cards in a straight have the form x,x+1,x+2,x+3,x+4,where x can be any of 10 ranks. There are then 4 choices for each card ofthe given ranks. This yields total choices. However,this count includes the straight flushes. Removing the 40 straightflushes leaves us with 10,200 straights.
In forming a 3-of-a-kind hand, there are 13 choices for the rank of thetriple, and there are choices for the ranks of theother 2 cards. There are 4 choices for the triple of the given rank andthere are 4 choices for each of the cards of the remaining 2 ranks.Altogether, we have 3-of-a-kind hands.
Next we consider two pairs hands. There are choices for the two ranks of the pairs. There are 6 choices for eachof the pairs, and there are 44 choices for the remaining card. Thisproduces hands of two pairs.
Now we count the number of hands with a pair. There are 13 choices forthe rank of the pair, and 6 choices for a pair of the chosen rank. Thereare choices for the ranks of the other 3 cardsand 4 choices for each of these 3 cards. We have hands with a pair.
We could determine the number of high card hands by removing the handswhich have already been counted in one of the previous categories.Instead, let us count them independently and see if the numbers sumto 2,598,960 which will serve as a check on our arithmetic.
A high card hand has 5 distinct ranks, but does not allow ranks of theform x,x+1,x+2,x+3,x+4 as that would constitute a straight. Thus, thereare possible sets of ranks from which we remove the10 sets of the form .This leaves 1,277 sets of ranks.For a given set of ranks, there are 4 choices for each cardexcept we cannot choose all in the same suit. Hence, there are1277(45-4) = 1,302,540 high card hands.
Number Of Distinct Poker Hands
If we sum the preceding numbers, we obtain 2,598,960 and we can be confidentthe numbers are correct.
Here is a table summarizing the number of 5-card poker hands. Theprobability is the probability of having the hand dealt to you whendealt 5 cards.
| hand | number | Probability |
| straight flush | 40 | .000015 |
| 4-of-a-kind | 624 | .00024 |
| full house | 3,744 | .00144 |
| flush | 5,108 | .0020 |
| straight | 10,200 | .0039 |
| 3-of-a-kind | 54,912 | .0211 |
| two pairs | 123,552 | .0475 |
| pair | 1,098,240 | .4226 |
| high card | 1,302,540 | .5012 |
last updated 12 January 2000