List Of Poker Hands From Best To Worst
Knowing what beats what in poker or Texas Hold’em is an important early step in learning the game. To help you out, I have provided for you an attractive printable or downloadable “cheat sheet” for both 5 card hand rankings as well as top 24 pre-flop starting hands.
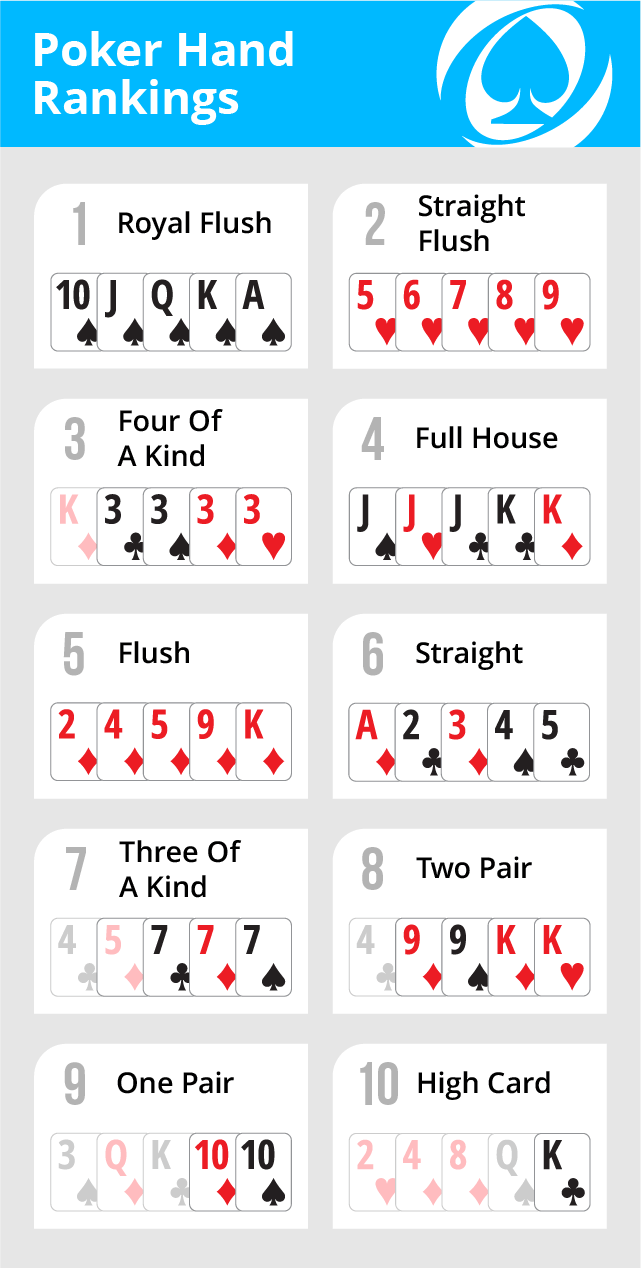
Poker hands ranked from best to worst:
Marathon en relais de 2, 4 ou 6 coureurs. List of best starting poker hands, list of poker hands from best to worst.
- Royal Flush
- Straight Flush
- Four of a Kind
- Full House
- Flush
- Straight
- Three of a Kind
- Two Pair
- One Pair
- High Card

- Poker Hand Rankings: Best to Worst 1. Ace-King-Queen-Jack-Ten, all of the same suit 2. Five consecutive cards, all of the same suit 3. Four cards of the same rank (also known as quads) 4.
- The best poker players often play the worst cards well. They know how to bluff and outmaneuver their opponents through careful positioning, betting, raising, and applying psychological pressure. One of the most important tips in poker is the following: Only play strong starting hands.
- The table includes all cards’ combinations in the game arranged from the best in the top to the worst in the bottom. Royal Flush, Straight Flush, Four of a Kind, Full House, Flush, Straight, Three of a Kind, Two Pairs and Pair - all hands are represented in this table.
To make things easier on you, I have included some handy charts that can be used to reference during play or even printed out.
Poker Hand Rankings Chart
Never forget what beats what again. Feel free to save this to your phone/tablet/computer or print the chart out.
Click below to download a high-quality PDF that includes a printable copy of both the showdown and pre-flop hand rankings.
The Top 24 Hold’Em Starting Hand Rankings
To help you out, I have also included the top 24 no-limit hold’em starting hands to give you a further idea of what beats what in poker. I based this list on both raw equities as well as post-flop playability.
I have used over 10 years of experience in both tournaments and cash games to compile this info. You get to benefit from my hard work!
How These Hands Were Determined

I took a look at a few of the pre-flop hand ranking charts out there and, while most appeared to get it right for the most part, there seemed to be something off.
The thing is, everyone always does pretty well on the top 5 or 6 hands. However, after that things get a bit murkier
So, what really matters when it comes to weighing hand strength? I decided to take a close look at the problem. Using the knowledge I’ve gained over the past few years, I tried to come up with a better way of codifying hand rankings.
Determining the Overall Playability of Each Hand
I decided to go about it from a logical standpoint. When deciding whether to play a hand or not, what are the factors a strong player considers before acting
So, I decided that there are basically two main factors to consider in determining the strength of a particular pre-flop hand. And, since equity is the tool we use to rank the value of hands I just had to figure out what type of equities matter most and then apply it to each factor
Once I was able to define which equities to consider, it just took a bit of math.
1. Pre-Flop Equity
The first equity I decided to factor in is a hand’s raw pre-flop equity. I mean, sometimes you need to get all-in before the flop, right?
Of course, some hands will get all-in more frequently than others but for the sake of simplicity, raw equity against a strong range will give us a decent enough metric to come up with a comparative ranking.
2. Post-Flop Equity
Secondly, we need to factor in how a hand does post-flop. There’s no doubt, that certain hands play much better after the flop than others.
To calculate how well a hand does after the flop I looked at what post-flop hands tend to get all-in most of the time in a post-flop scenario. This includes the strongest made hands, including top pair and better, as well as strong draws.
Once I was able to figure out what hands are likely to get all-in, I just had to figure out the equity of every hand versus that range on a random flop.
Compiling the Final List
Doing these kinds of calculations by hand would be extremely difficult and time-consuming. Luckily, there is a software program called Cardrunner’s EV that does the math for me.
After I figured out both the raw pre-flop equity and the likely flop equity of each hand, I just used excel to average them. That data was used to compile the rankings.
Here are the final equity percentages:
Which Poker Starting Hand Ranges Should I Use?
Knowing which hands to open raise is important to your success. Don’t worry, I’ve got you covered.
Free Basic Poker Strategy Charts
I have built charts that provide you profitable opening ranges from every position. As a bonus, the charts also include what to do at every decision point possible for playing a 20 to 40 big blind stack
The guide will give you an excellent starting point for playing No-Limit Texas Hold’em and will get you off on the right foot by allowing you to play fundamentally sound poker right now!
FAQ
What if my opponent and I have the same hand at showdown ?
If more than one player has the same hand then you have to follow the tie-breaker rules to determine the winner.
If two or more players have a flush or straight
In the case where two players have a flush or straight, the person who has the highest card in their hand wins. For example, T9876 beats 76543.
If two or more players have a full house
In the case of multiple full houses, the player with the highest “trips” as part of their full house wins. For example, TTT22 beats 555AA.
What if two or more players have the same pair or two pair?
If multiple players have exactly the same two pair, the highest kicker is used to determine the winner. For example, JJ66Q beats JJ66T.
The same process is used for one-pair. The next highest kicker is used. If that is the same, you use the next highest kicker. So on and so forth until the tie is broken. For example, AAK85 beats AAK84.
Who wins if more than one person has the same high card?
Similarly to one pair and two-pair hands, you use the next highest kicker to determine the winner. You keep moving on to the next kicker until a winner is determined. For example, KT763 beats KT753.
Which is better, trips or two-pair?
Three of a kind beats two-pair. It also beats a pair and high card.
Which is better, a flush or a straight?
A flush beats a straight. It also beats three of a kind, two pair, a pair, and high card.
What is the worst hand in poker?
The worst hand against multiple players is 72 offsuit. The worst hand heads-up is 32o.
What are the odds of getting a Royal Flush in Texas Hold’em?
A royal flush is extremely rare. You can only expect to get a royal flush once every 650,000 hands. That doesn’t mean it’s guaranteed. Personally, I have played well over 5 million hands and have only had one royal using both cards.
Final Thoughts
I hope this article has helped you learn more about how hand rankings work in poker. If you want to learn about basic poker strategy, be sure to check out my detailed no-limit hold’em basic tutorial.
This post works with 5-card Poker hands drawn from a standard deck of 52 cards. The discussion is mostly mathematical, using the Poker hands to illustrate counting techniques and calculation of probabilities
Working with poker hands is an excellent way to illustrate the counting techniques covered previously in this blog – multiplication principle, permutation and combination (also covered here). There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million). The probability of obtaining a given type of hands (e.g. three of a kind) is the number of possible hands for that type over 2,598,960. Thus this is primarily a counting exercise.
___________________________________________________________________________
Preliminary Calculation
Usually the order in which the cards are dealt is not important (except in the case of stud poker). Thus the following three examples point to the same poker hand. The only difference is the order in which the cards are dealt.
These are the same hand. Order is not important.
The number of possible 5-card poker hands would then be the same as the number of 5-element subsets of 52 objects. The following is the total number of 5-card poker hands drawn from a standard deck of 52 cards.
The notation is called the binomial coefficient and is pronounced “n choose r”, which is identical to the number of -element subsets of a set with objects. Other notations for are , and . Many calculators have a function for . Of course the calculation can also be done by definition by first calculating factorials.
Thus the probability of obtaining a specific hand (say, 2, 6, 10, K, A, all diamond) would be 1 in 2,598,960. If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of all diamond cards? It is
This is definitely a very rare event (less than 0.05% chance of happening). The numerator 1,287 is the number of hands consisting of all diamond cards, which is obtained by the following calculation.
The reasoning for the above calculation is that to draw a 5-card hand consisting of all diamond, we are drawing 5 cards from the 13 diamond cards and drawing zero cards from the other 39 cards. Since (there is only one way to draw nothing), is the number of hands with all diamonds.
If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of cards in one suit? The probability of getting all 5 cards in another suit (say heart) would also be 1287/2598960. So we have the following derivation.
Thus getting a hand with all cards in one suit is 4 times more likely than getting one with all diamond, but is still a rare event (with about a 0.2% chance of happening). Some of the higher ranked poker hands are in one suit but with additional strict requirements. They will be further discussed below.
Another example. What is the probability of obtaining a hand that has 3 diamonds and 2 hearts? The answer is 22308/2598960 = 0.008583433. The number of “3 diamond, 2 heart” hands is calculated as follows:
One theme that emerges is that the multiplication principle is behind the numerator of a poker hand probability. For example, we can think of the process to get a 5-card hand with 3 diamonds and 2 hearts in three steps. The first is to draw 3 cards from the 13 diamond cards, the second is to draw 2 cards from the 13 heart cards, and the third is to draw zero from the remaining 26 cards. The third step can be omitted since the number of ways of choosing zero is 1. In any case, the number of possible ways to carry out that 2-step (or 3-step) process is to multiply all the possibilities together.
List Of Poker Hands From Best To Worst
___________________________________________________________________________
The Poker Hands
Here’s a ranking chart of the Poker hands.
The chart lists the rankings with an example for each ranking. The examples are a good reminder of the definitions. The highest ranking of them all is the royal flush, which consists of 5 consecutive cards in one suit with the highest card being Ace. There is only one such hand in each suit. Thus the chance for getting a royal flush is 4 in 2,598,960.
Royal flush is a specific example of a straight flush, which consists of 5 consecutive cards in one suit. There are 10 such hands in one suit. So there are 40 hands for straight flush in total. A flush is a hand with 5 cards in the same suit but not in consecutive order (or not in sequence). Thus the requirement for flush is considerably more relaxed than a straight flush. A straight is like a straight flush in that the 5 cards are in sequence but the 5 cards in a straight are not of the same suit. For a more in depth discussion on Poker hands, see the Wikipedia entry on Poker hands.
The counting for some of these hands is done in the next section. The definition of the hands can be inferred from the above chart. For the sake of completeness, the following table lists out the definition.
Definitions of Poker Hands
| Poker Hand | Definition | |
|---|---|---|
| 1 | Royal Flush | A, K, Q, J, 10, all in the same suit |
| 2 | Straight Flush | Five consecutive cards, |
| all in the same suit | ||
| 3 | Four of a Kind | Four cards of the same rank, |
| one card of another rank | ||
| 4 | Full House | Three of a kind with a pair |
| 5 | Flush | Five cards of the same suit, |
| not in consecutive order | ||
| 6 | Straight | Five consecutive cards, |
| not of the same suit | ||
| 7 | Three of a Kind | Three cards of the same rank, |
| 2 cards of two other ranks | ||
| 8 | Two Pair | Two cards of the same rank, |
| two cards of another rank, | ||
| one card of a third rank | ||
| 9 | One Pair | Three cards of the same rank, |
| 3 cards of three other ranks | ||
| 10 | High Card | If no one has any of the above hands, |
| the player with the highest card wins |
___________________________________________________________________________
Counting Poker Hands
Straight Flush
Counting from A-K-Q-J-10, K-Q-J-10-9, Q-J-10-9-8, …, 6-5-4-3-2 to 5-4-3-2-A, there are 10 hands that are in sequence in a given suit. So there are 40 straight flush hands all together.
Four of a Kind
There is only one way to have a four of a kind for a given rank. The fifth card can be any one of the remaining 48 cards. Thus there are 48 possibilities of a four of a kind in one rank. Thus there are 13 x 48 = 624 many four of a kind in total.
List Of Poker Hands From Best To Worst Hits
Full House
Let’s fix two ranks, say 2 and 8. How many ways can we have three of 2 and two of 8? We are choosing 3 cards out of the four 2’s and choosing 2 cards out of the four 8’s. That would be = 4 x 6 = 24. But the two ranks can be other ranks too. How many ways can we pick two ranks out of 13? That would be 13 x 12 = 156. So the total number of possibilities for Full House is
Note that the multiplication principle is at work here. When we pick two ranks, the number of ways is 13 x 12 = 156. Why did we not use = 78?
Flush
There are = 1,287 possible hands with all cards in the same suit. Recall that there are only 10 straight flush on a given suit. Thus of all the 5-card hands with all cards in a given suit, there are 1,287-10 = 1,277 hands that are not straight flush. Thus the total number of flush hands is 4 x 1277 = 5,108.
Straight
There are 10 five-consecutive sequences in 13 cards (as shown in the explanation for straight flush in this section). In each such sequence, there are 4 choices for each card (one for each suit). Thus the number of 5-card hands with 5 cards in sequence is . Then we need to subtract the number of straight flushes (40) from this number. Thus the number of straight is 10240 – 10 = 10,200.
Three of a Kind
There are 13 ranks (from A, K, …, to 2). We choose one of them to have 3 cards in that rank and two other ranks to have one card in each of those ranks. The following derivation reflects all the choosing in this process.

Two Pair and One Pair
These two are left as exercises.
High Card
The count is the complement that makes up 2,598,960.
The following table gives the counts of all the poker hands. The probability is the fraction of the 2,598,960 hands that meet the requirement of the type of hands in question. Note that royal flush is not listed. This is because it is included in the count for straight flush. Royal flush is omitted so that he counts add up to 2,598,960.
Probabilities of Poker Hands
| Poker Hand | Count | Probability | |
|---|---|---|---|
| 2 | Straight Flush | 40 | 0.0000154 |
| 3 | Four of a Kind | 624 | 0.0002401 |
| 4 | Full House | 3,744 | 0.0014406 |
| 5 | Flush | 5,108 | 0.0019654 |
| 6 | Straight | 10,200 | 0.0039246 |
| 7 | Three of a Kind | 54,912 | 0.0211285 |
| 8 | Two Pair | 123,552 | 0.0475390 |
| 9 | One Pair | 1,098,240 | 0.4225690 |
| 10 | High Card | 1,302,540 | 0.5011774 |
| Total | 2,598,960 | 1.0000000 |
___________________________________________________________________________
2017 – Dan Ma